
一次方程式の場合
例えば、データ(x1,y1)、(x2,y2)、……………..、(xn,yn)が与えられた時、最も近似する直線を求めましょうという場合に使う方法。
こんな感じ。
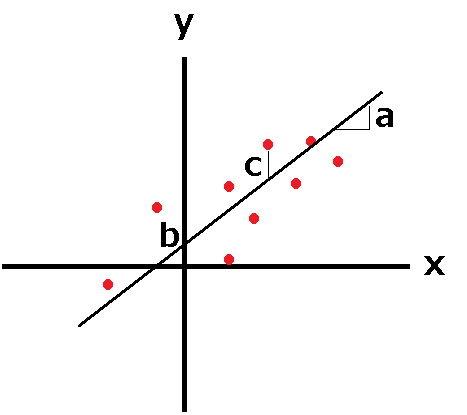
y = a*x + b <-このa、bが知りたい!
誤差/残差 (c = |yi – a*xi -b|) の二乗和
$$J = \displaystyle \sum_{i = 1 }^{ n }(y_i – a*x_i -b)^2 = \sum_{i = 1 }^{ n }(y_i^2 – 2*a*y_i*x_i + a^2*x_i^2 – 2*b*y_i + 2*b*a*x_i+b^2)$$
Jを最小にするa、bを求める->変数a、bで偏微分したものが0になればよい…..と考える。
$$ \frac {\partial J }{\partial a} = -2\sum_{i = 1 }^{ n }y_ix_i + 2a\sum_{i = 1 }^{ n }x_i^2 + 2b\sum_{i = 1 }^{ n }x_i = 0$$
$$\begin{eqnarray} \frac {\partial J }{\partial b} = -2\sum_{i = 1 }^{ n }y_i + 2a\sum_{i = 1 }^{ n }x_i + 2\sum_{i = 1 }^{ n }b \\= -2\sum_{i = 1 }^{ n }y_i + 2a\sum_{i = 1 }^{ n }x_i + 2nb = 0\end{eqnarray}$$
Σの演算やnは既知数なので、このa、bに関する連立方程式を解いてa、bの値を求めればよい…..ということになる。
標準偏差と共分散で解く….という手もあるが、今回はパス
Leave a Reply