勾配(gradient)*1
xy平面上の等高線をz軸方向に立ち上げてお山を作ってみます。
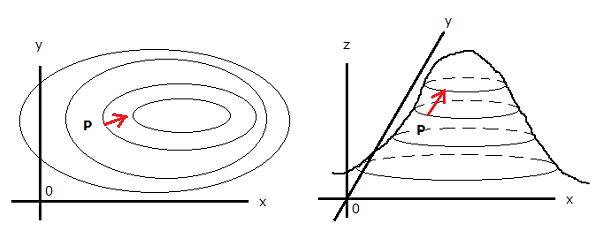
お山の中腹にいる人(P)がある方向に進むとします。
$$このベクトル:grad f はxy平面に矢印として表され、平面上の各点で方角を表しているします。$$
スカラー場:f(x,y)
$$勾配ベクトル:grad f = \nabla f = \left( \frac {\partial f}{\partial x},\frac {\partial f}{\partial y}\right)について$$
①grad f は、等高線と直交する
②grad f は、傾きが一番大きくなる向きを表す
③|grad f |は、傾きの最大値を表す
つまり、Pはgrad fの指し示す方角に進む時、傾きが一番きつくなります。
なんで?かというと……
①
等高線を媒介変数tを用いて表し、点(x(t),y(t))の集合とみなします。
等高線はf(x,y) = C(定数)と表せます(等高線だからね)。
f(x(t),y(t)) = C
tで微分すると…..
$$\frac{\partial f(x(t),y(t))}{\partial x} \cdot \frac{dx(t)}{dt} + \frac {\partial f(x(t),y(t))}{\partial y} \cdot \frac{dy(t)}{dt} = 0\hspace{55pt }$$
$$左辺をgrad f = \left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right)と等高線の接線 \left( \frac{dx}{dt},\frac{dy}{dt} \right)の内積とみなすと$$
内積 = 0で、両者は直交していることになります。
つまり、grad f は等高線の法線ベクトル
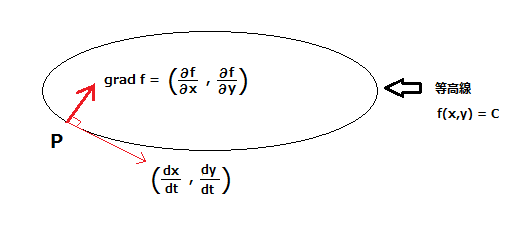
②、③
点(a,b,f(a,b))での最大の傾きを求めてみます。
x軸とθの角をなす直線L->点(a+tcosθ,b+tsinθ,0)の集合を設定
Lを含みxy平面に垂直な面Πで曲面(お山)を切断すると、切り口には曲線が現れます。
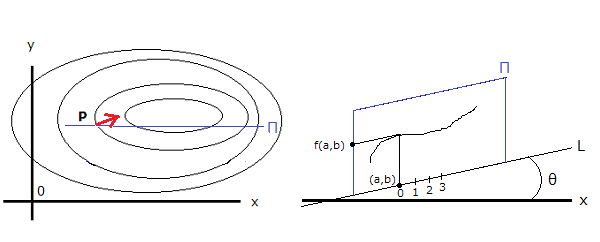
この曲線の(a,b,f(a,b))での傾きを求めてみます。
媒介変数t=1に対応する点には1、t=2に対応する点に2、というようにL上に目盛をふると、
単位ベクトル
|(cosθ,sinθ)| = 1
ですから、Lにはx軸y軸と同じ間隔で目盛がふられます。
切り口の曲線は、平面Π (tz座標平面)でtの関数として
z = f(a+tcosθ,b+tsinθ)
と表わされます。
従って、切り口での曲線の傾きは f(a+tcosθ,b+tsinθ)を媒介変数tで微分することで得られます。
f(x,y)で、x = a + tcosθ、y = b + tsinθとおいているので、傾きは
$$\begin{eqnarray}\frac{df(a+tcosθ,b+tsinθ)}{dt} &=& \frac{\partial f}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dt} \\ &=& \frac{\partial f}{\partial x}cosθ + \frac{\partial f}{\partial y}sinθ \end{eqnarray}$$
$$ここでgrad f = \left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right)をxy平面のベクトルとして捉え、これとx軸のなす角をαとすると$$
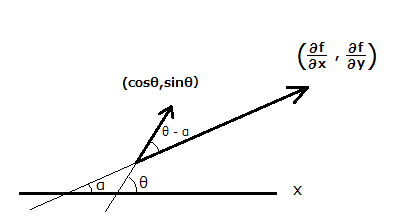
2つのベクトルのなす角度の公式を思い出しましょう。
$$\frac{\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}} {| \overrightarrow{\mathrm{OA}}| \cdot|\overrightarrow{\mathrm{OB}}|} = \cos\left(\angle \mathrm{AOB}\right)$$
傾きを内積で表してみます。
$$ \frac{\partial f}{\partial x}cosθ + \frac{\partial f}{\partial y}sinθ = \left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right) \cdot (cosθ,sinθ)$$
傾きベクトルと単位ベクトルとのなす角度を公式にあてはめて、
$$\frac {\left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right) \cdot (cosθ,sinθ)}{ \left|\left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right)\right| \vert cosθ,sinθ)\vert} = cos(θ – α) $$
従って傾きはこうなる。
$$\begin{eqnarray}\frac{\partial f}{\partial x}cosθ + \frac{\partial f}{\partial y}sinθ &=& \left|\left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right)\right| \vert cosθ,sinθ)\vert cos(θ – α) \\ &=& \left|\left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right)\right| cos(θ – α) \end{eqnarray}$$
-1 ≦ cos(θ – α) ≦ 1
傾きが最大になるのはθ = α、すなわちgrad fの方角で切断したときで
最大値は|grad f|
ここでは最大値について記述していますが、機械学習でいう勾配は「お山」を逆さにして考えるとイメージしやすい。求めるのは最小値。
テンソル(tensor)
アタリマエに使うには、ある程度の訓練と慣れが必要です。
「テンソルは多次元の配列で、階数0のスカラーや階数1のベクトル、階数2の行列などの階数nへの一般化を与えているものと見なされる。テンソルの「成分」は配列の要素の値によって与えられることになる。この考えはテンソル場として一般化され、テンソルの成分として関数やその微分が取り扱われるようになる。」(Wikipedia)
テンソル->型を有するn次元の多次元配列
このように記述することで,「n次元の多次元配列」の要素に任意の値を設定することができます.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import tensorflow as tf row = 3 col = 4 # 定数 constant_tsr = tf.constant(1) # 全て 0 の要素からなるテンソル zeros_tsr = tf.zeros([row, col]) # 全て 1 の要素からなるテンソル ones_tsr = tf.ones([row, col]) # 全て第二引数で指定した定数の要素からなるテンソル filled = tf.fill([row, col], 5) # 0~10 の一様分布乱数の要素からなるテンソル randunif_tsr = tf.random_uniform([row, col], minval=0, maxval=10) # 平均 0.0,標準偏差 1.0 の正規分布に従う乱数の要素からなるテンソル randnorm_tsr = tf.random_normal([row, col], mean=0.0, stddev=1.0) |
テンソルの演算
四則演算ならこんな感じ
|
1 2 3 4 5 6 7 |
x = tf.constant(6) y = tf.constant(2) add_op = tf.add(x, y) # 定数の足し算 sub_op = tf.subtract(x, y) # 定数の引き算 mul_op = tf.scalar_mul(x, y) # 定数の掛け算 div_op = tf.divide(x, y) # 定数の割り算 |
では、なぜテンソルなのかは、この方のブログ参照
*1
勾配については「一般相対性理論を一歩一歩数式で理解する」(石井俊全 著)からほぼ引用
この本はテンソルを理解したいという(数学寄り、物理寄り双方の)方にもお奨め。
もし買う気になったら、正誤表はこちら(なんでこうなるんだ?としばし悩む手間が省けます)
AI用語 メモ
Leave a Reply