ちょっと引っかかるところとかをメモっておきました
編集中で、時々更新されます。
計算グラフ(computational graph) : 演算とデータをノード(node)とエッジ(edge)で表現する方法 : 参照
重み(weight): 入力された値をどれくらい強化/減衰させるかを決める変数
バイアス(bias):出力を制御する(させ易くしたり逆にさせ難くくする)因子、あるいは出力の傾向の高さを表す量
活性化関数(activation function): 受け取った値を、どのように次の層へ渡すかを定義した関数
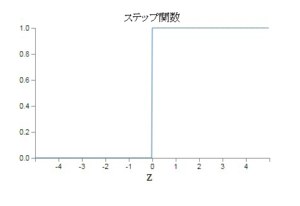
パーセプトロン(perceptron)、あるいは単純/単層パーセプトロンでは、ステップ(step,staircase)関数
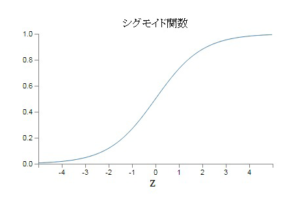
ニューラルネットワーク(neural network)、あるいは多層パーセプトロン(MLPs)では、シグモイド(sigmoid)、ソフトマックス(softmax)、tanh、ReLU(ランプ)など
の非線形(unlinear)関数(function)が使われる
注:単純/単層(single)パーセプトロン、多層(multiple)パーセプトロンという表現はこのサイトでは使いません。
活性化関数に非線形関数を使う理由は?
線形の活性化関数では非線形分離できないから。
逆に言うと、非線形な関数なら、線形分離不可能な問題や線形近似できない問題等を解くことができるから。
誤差(error):ニューラルネットワークから出力した値と、実際の値との間の差異(difference)
全結合層(fully connected layer,inner product layer) : すべてのノードが次の層のすべてのノードに繋がっている層の事
ハイパーパラメーター(hyper parameter):学習アルゴリズムからは直接さわれないパラメーター(人間系の変数)
世代(epoch) : 一つの訓練データを学習させる回数(過学習を起こさずに、かつ訓練精度と予測精度が共に良い回数を見つけることが肝要)
ミニバッチサイズ(mini batch size):
学習率、訓練率(learning rate):
ライプニッツ則(Leibniz rule):関数の積の微分(differentiation)
{f(x)g(x)}’ = f'(x)g(x) + f(x)g'(x)
あるいは
$$\frac{d}{dx}( u(x) \cdot v(x))= u(x) \cdot \frac{dv(x)}{dx} + v(x) \cdot \frac{du(x)}{dx}\hspace{100pt } $$
連鎖律(chain rule):合成関数の微分
{f(g(x))}’ = f'(g(x))g'(x)
あるいは.
$$y = f(u),u = g(x) \hspace{ 220pt } $$ $$ \frac {dy}{dx} = \frac {dy}{du} \frac {du}{dx}\hspace{ 250pt } $$
偏微分についても
$$z = f(u),u = g(x,y)\hspace{ 220pt }$$
$$\frac{\partial z}{\partial x} = \frac {\partial z}{\partial u} \frac {\partial u}{\partial x} \hspace{ 250pt }$$
$$\frac{\partial z}{\partial y} = \frac {\partial z}{\partial u} \frac {\partial u}{\partial y} \hspace{ 250pt }$$
$$\frac{d f(x(t),y(t))}{dt} = \frac{\partial f(x(t),y(t))}{\partial x} \cdot \frac{dx(t)}{dt} + \frac {\partial f(x(t),y(t))}{\partial y} \cdot \frac{dy(t)}{dt}$$
エンコード(encode):データ(data)に特定の方法で、後で元の(あるいは類似の)データに戻せるような変換(conversion)を加えること。
最小二乗法、最小自乗法( least squares method):
誤差を含んだ値から, 最もフィットする関数を計算する手法
コスト(cost)関数(損失関数、目的関数、誤差関数):重みとバイアスを変数に持つ関数。この関数を最小にする重みとバイアスを見つけることが眼目になる。
例:二次コスト関数
$$C(w,b) = \frac{1}{2n} \sum_x \| y(x) – a \|^2$$
$$C(w,b)\approx 0 となるw,bは何? $$
勾配降下法(gradient descent):
これ自体は最小値を求める手法であって、機械学習のためのものというわけではない。コスト関数を最小化するアイデアとして関数に勾配降下法を適用してみようというのが機械学習の眼目。
->最急降下法(steepest descent)
->確率的勾配降下法(stochastic gradient descent, SGD)
->ミニバッチ確率的勾配降下法
確率的:通常の勾配降下法では訓練入力の数が非常に大きい場合はとても時間が掛かり、その結果学習は非常に遅くなってしまう。そこで、訓練入力から無作為に抽出した小さな標本群 を計算して勾配 を推定する。小さな標本群の平均を取ることで速やかに正しい勾配 を推定でき、勾配降下法が高速化できる。
勾配を高速に計算するアルゴリズム(algorithm)が逆伝播
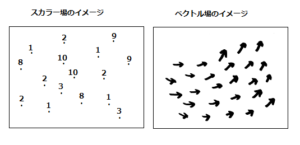
勾配:スカラー(scalar)場(field)からベクトル(vector)場(field)を作り出す仕組み
あるいはスカラー関数の各成分の傾き(gradient,slope)
スカラー場:f(x,y,z)
$$ベクトル場:grad f = \nabla f = \left( \frac {\partial f}{\partial x},\frac {\partial f}{\partial y},\frac {\partial f}{\partial z}\right)$$
スカラー場:0階のテンソル(tensor)場
ベクトル場:1階のテンソル(tensor)場
場(field)のイメージ
スカラー場の各点は単位を与えると分かりやすい、℃とかmとか…
ベクトル場の矢印に単位を与えるとしたらm/sなど
勾配(gradient)は地図の等高線をイメージした説明が理解しやすいようですし、テンソルに関しても定義の仕方によっては泥沼にはまりやすいようで、”ニューラルネットをコードに落とし込む場合は……”という限定での説明の方がピンとくると思うので、別ページにメモっておきます。
あるいは、テンソルについても数学なんて知らないよ…という方は、「数学する身体」(森田真生)の第二章あたりを読むと”何となく腑に落ちるかも”…です。
フィードフォワードニューラルネットワーク(feedforward neural network);
再帰型ニューラルネットワーク(recurrent neural network):
逆伝播(backpropagation):
L : ニューラルネットワークの層数(number of layers)
$$出力層での誤差\delta^Lに関する式(equation)\hspace{ 75pt }$$
$$\delta^L = \nabla_aC \odot \sigma ‘ (z^L)$$
$$誤差\delta^Lの次層での誤差\delta^{L+1}に関する式(equation)\hspace{ 35pt }$$
$$\delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma ‘ (z^l)$$
$$任意のバイアスに関するコストの変化率の式(equation)\hspace{ 15pt }$$
$$\frac{\partial C}{\partial b_j^l} = \delta_j^l$$
$$任意の重みについてのコストの変化率の式(equation)\hspace{ 20pt }$$
$$\frac{\partial C}{\partial w_{jk}^l} = a_k^{l -1}\delta_j^l$$
$$ \odot :アダマール積(Hadamard \hspace{ 3pt }product)/シューア積 \hspace{ 80pt }$$
例
$$\left({\begin{array}{cc} a _{11}&a _{12}\\ a _{21}&a _{22}\\ a _{31}&a _{32}\\ \end{array}}\right) \odot \left({\begin{array}{cc} b _{11}&b _{12}\\ b _{21}&b _{22}\\ b
_{31}&b _{32} \end{array}}\right) =\left({\begin{array}{cc} a _{11}\,b _{11}&a _{12}\,b _{12}\\ a _{21}\,b _{21}&a _{22}\,b _{22}\\ a _{31}\,b _{31}&a _{32}\,b _{32}
\end{array}}\right)$$
添え字の読み方
$$w_{jk}^l (l−1)番目の層のk番目のニューロンから、 l番目の層の\\ j番目のニューロンへの接続に対する重み$$
$$a_j^l l番目の層のj番目のニューロンの活性\hspace{ 70pt }$$
$$b_j^l l番目の層のj番目のニューロンのバイアス\hspace{ 60pt }$$
要するに…….ニューラルネットワークと深層学習によれば
逆伝播の目標はニューラルネットワーク中の任意の重みwまたはバイアスbに関するコスト関数Cの偏微分、すなわち∂C/∂wと∂C/∂bの計算です。
逆伝播は多変数関数の微分で利用される連鎖律をシステマチックに適用する事で、コスト関数の勾配を計算する方法と見る事ができます。 それが逆伝播の正体であり、残りは些細な部分です。
逆伝播の賢い所は、たった1回の順伝播とそれに続く1回の逆伝播ですべての偏微分∂C/∂wjを同時に計算できる点です。
クロス(交差)エントロピー(cross entropy):コスト関数の一種。
過学習、過適合(overfitting):
ノルム(norm): 大きさを表す量(機械学習で使う色々な距離の概念のうちの1つ)
実数上のベクトル空間 V
任意の x , y∈V と任意の実数(スカラー)a
$$\|\overrightarrow{x}\|=0\iff \overrightarrow{x}=0\hspace{ 240pt }$$
$$\|a\overrightarrow{x}\|=|a|\|\overrightarrow{x}\| \hspace{ 270pt }$$
$$\|\overrightarrow{x}\|+\|\overrightarrow{y}\|\geq \|\overrightarrow{x}+\overrightarrow{y}\| \hspace{ 230pt }$$
正規(正則)化(regularization):過適合を軽減する手法。
L1、L2、ドロップアウト(dropout)、……
$$L^1 =\displaystyle \sum_{ i = 1 }^{ n } |x_i|$$
$$L^2 = \displaystyle \sqrt {\sum_{ i = 1 }^{ n } x_i^2}$$
正規化(正則化)と標準化は厳密に区別される
画像認識用に学習用画像データを「そろえる」場合も正規化という
畳み込みニューラルネットワーク(convolutional neural network)で使われる重要な3つのアイデア
局所受容野(local receptive field)、特徴マップ(feature map):
重み(weight)とバイアス(bias)の共有:
プーリング(pooling):
訓練データ(training data)の拡張:水増し
カーネル(kernel)、フィルター(filter):共有重みと共有バイアス
畳み込み(convolution):
* : 畳み込み演算
$$a^1 = \sigma(b + w*a^0)$$
線形(linear):関数 f が線形の場合以下が成り立つ。プロットしたグラフは直線。
f(x + y) = f(x) + f(y)
f(k*x) = k*f(x)
従って、非線形とはこういう関係が成り立たない….ということ。
例:単純な非線形関数
f(x) = x + 1
f(k*x) = k*x + 1
k*f(x) = k*x + k
従ってこの場合は、f(k*x) = k*f(x)が成り立たない
線形分離(識別)可能(linearly separable):幾何的には、ふたつの点の集合(set)が二次元平面上にあるとき、それらの集合を一本の直線で分離できること(境界線を引くイメージ)。
3次元以上の場合を含めて一般化すると、n次元空間(space)上のふたつの点の集合をn-1次元の超平面(hyperplane)で分離できる…ということ。
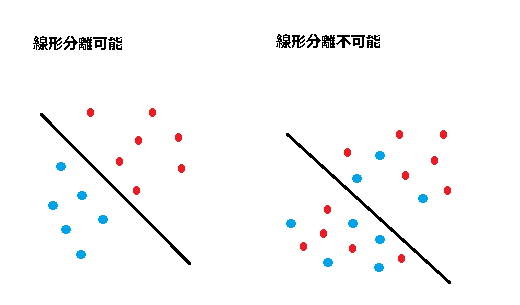
入力を超空間の座標、出力をその点の属性と捉えると、属性で点を分類したときに線形分離可能であればパーセプトロンで問題を解くことができる(教師あり学習)。
SVM(Support Vector Machine : サポートベクターマシン):線形識別器の一種
●普遍性定理 : 計算したい関数が何であろうとも、その計算を行えるニューラルネットワークが存在する
●畳込みニューラルネットワークは画像に対して並進不変性がある
アドホック(ad hoc)な:暫定的な、特定の目的のための、その場限りの
ヒューリスティック(heuristic):経験則(の)、試行錯誤(的な)という意味。必ず正しい答えを導けるわけではないが、ある程度のレベルで正解に近い解を得ることができる方法。
Leave a Reply