点の分布を面で捉えようという感じ。
標準偏差楕円も参照
QGISでtokyoデータのコンビニデータ(cvs_jgd2011_9.shp)と行政区画のポリゴン(tokyo23ku_jgd2011_9.shp)は読み込み済みとします。
メニュで、プロセッシング -> ツールボックスを開いて、
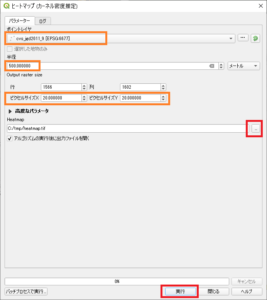
データ補間 -> ヒートマップ(カーネル密度推定)をダブルクリック
ポイントレイヤ -> cvs_jgd2011_9
半径 -> 500m
ピクセルサイズ -> 20
出力ラスター名 -> 適当にheatmap
で、実行。
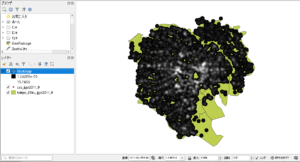
こんな感じ。
背景の行政区画ポリゴンの境界線を見やすくします。
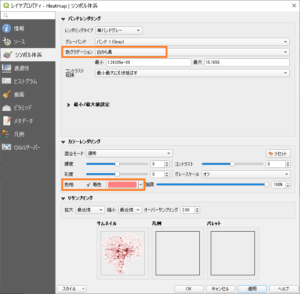
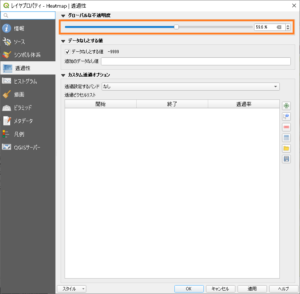
Heatmapのプロパティを開いて、
シンボル体系
色グラデーション -> 白から黒
色相 -> 明るめの暖色系
透過性
不透明度 -> 半分くらい
コンビニの表示は外しておきます。
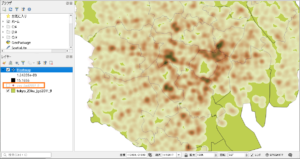
こんな感じ。
半径の値(バンド幅)を広くとったカーネルは広域的傾向把握に有効である。
一方で、局地的な値への対応が難しくなる。そのため、バンド幅の設定には注意する必要がある….だそうです。
i=1,・・・・・,nまでについて、観測値Xiが与えられている時、xにおけるカーネル密度の
推定値は以下のように求められる。
$$\Huge{\tilde{f_K}(x) = \frac{1}{nh}\sum_{ i = 1 }^{ n } K\begin{pmatrix} \frac{x – X_i}{h}\end{pmatrix}}$$
ただし、hはバンド幅。
K(z)はカーネル関数で、以下がよく用いられる。
Gaussianカーネル
$$\Huge{K(z) = \frac{1}{\sqrt{2\pi}}e^\frac{-z^2}{2}}$$
Epanechnikovカーネル
$$\LARGE{\begin{eqnarray} K(z) = \begin{cases} \frac{3}{4}(1- \frac{1}{5}z^2)/\sqrt{5} & (if |z| < \sqrt{5})\\ 0 & (otherwise) \end{cases} \end{eqnarray}}$$
Rectangularカーネル
$$\LARGE{\begin{eqnarray} K(z) = \begin{cases} \frac{1}{2} & (if |z| < 1) \\ 0 & (otherwise) \end{cases} \end{eqnarray}} $$
カーネル関数はカーネルトリックとして機械学習でよく用いられる手法です。

Leave a Reply