MLSを対象にして、様々な種類のパスがチームのスタイルに与える影響をk平均法を使って分析したものです。
用語についてはAppendixを参照
USING K-MEANS TO LEARN WHAT SOCCER PASSING TELLS US ABOUT PLAYING STYLES
k平均法を使用して、サッカーのパスがプレイスタイルに関して何を語るのかを学ぶ
When you talk about a soccer team, you almost always talk about its style: high-pressing, possession-heavy, parking-the-bus, etc. A team’s style not only signifies how they play on the field but also reflects its coaching. Since there aren’t guidelines on how the style of the team should be defined, everyone uses their own rules and we can’t directly compare each other’s descriptions.
サッカーチームについて話すとき、ほとんどの場合、そのスタイルについて話します:ハイプレス、ポゼションの重視、しっかりしたディフェンスなど。チームのスタイルは、フィールドでのプレーの仕方を示すだけでなく、そのコーチングも反映します。チームのスタイルを定義する方法に関するガイドラインがないため、全員が独自のルールを使用し、互いの説明を直接比較することはできません。
An accurate quantitative description of the style is needed.It can help one to properly analyze not only the opponent’s team but also his/her own team.
With an accurate method to describe the style, one can scientifically evaluate if a training exercise is efficient at serving its purpose. We previously have used dimension reduction technique, t-SNE, to find MLS teams with similar styles based on the spatial distribution of activities and pass networks. This time we use a different method, k-means clustering of pass types, to quantitatively measure style, tactical specialization, and the influence of coaching on a team’s system.
スタイルの正確で定量的説明が必要です。相手チームだけでなく、自チームも適切に分析するのに役立ちます。スタイルを正確に記述する方法で、トレーニングの演習が目的を果たすのに効率的であるかどうかを科学的に評価できます。以前に、次元削減手法であるt-SNEを使用して、動きとパスネットワークの空間分布に基づいて、同様のスタイルを持つMLSのチームを見つけました。今回は、パスの種類のk平均法という別の方法を使用して、スタイル、戦術的な特化、チームのシステムに対するコーチングの影響を定量的に測定します。
K-means clustering of passes
パスのk平均法
We used k-means clustering of pass types to quantify the styles of the teams in MLS. K-means clustering is a machine learning algorithm that separates data points into a user selected (k) number of clusters based upon their similarities.If you think that two clusters define the groups you want, you will choose k=2. If you think it is 10, choose 10. In our case, after using the elbow method and visual inspection, we chose to classify passes into 64 different groups based upon how and where passes were made. We want to note that using k-means clustering has been used many other times to describe passing behavior in soccer (and we used it, in part, to classify player positions). We extended previous work by using z-scores to standardize the quantification of each pass group. Then by filtering pass clusters based on z-scores we can find characteristic pass patterns for every team.
パスの種類のk平均法を使用して、MLSのチームのスタイルを定量化しました。k平均法はデータポイントを、類似性に基づいてユーザーが選択した(k)個のクラスターに分離する機械学習アルゴリズムです。2つのクラスターが必要なグループを定義していると思われる場合は、k = 2を選択します。 10と思う場合は、10を選択します。今回の場合は、エルボー法と視覚化検証を使用した後、パスの種類と場所に基づいて、パスを64の異なるグループに分類することにしました。k平均法は、サッカーでのパスの動きを説明するために何度も使用されていることに注意してください(そして、プレーヤーの位置を分類するために一部使用しました)。z値(標準得点)を使用して各パスグループの定量化を標準化することにより、以前の作業を拡張しました。次に、z値に基づいてパスクラスターをフィルター処理することにより、すべてのチームの特徴的なパスパターンを見つけることができます。
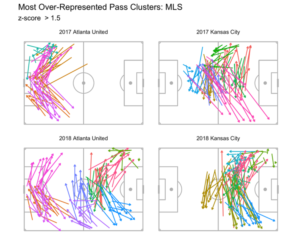
This visualization combines the features of both pass network and touch heatmap. It shows what areas a team utilizes the most and how (what type of passes) it uses to access this zone. For example, last season, Atlanta used long horizontal passes to stretch the opponent while Kansas City camped outside the opponent’s box with its possession dominance. By plotting distinctive pass types this way, we can also see how a team evolves under a coach. For instance, Tata Martino had clearly instructed how Atlanta played out from the back, however, it was a work-in-progress in the first year. They got the build-up part right but had trouble transitioning into the attack. With another full season to practice, they exploded into one of the best offensive teams in MLS history in their second season.
この視覚化は、パスネットワークとタッチヒートマップの両方の機能を組み合わせたものです。チームが最も利用しているエリアと、このゾーンへのアクセスにどのように(どのタイプのパスを)使用しているかを示します。たとえば、昨シーズン、アトランタは対戦相手を引き伸ばすために長い縦パスを使用しましたが、カンザスシティはポゼッションで相手のボックスの外側に陣取っていました。このように特徴的なパスタイプをプロットすることで、監督の下でチームがどのように進化するかを確認することもできます。たとえば、タタ・マルティーノはアトランタが後ろからどのようにプレーするかを明確に指示していましたが、最初の年はまだ道半ばでした。ビルドアップ部分は正しく行われましたが、攻撃への移行に問題がありました。もう1つのフルシーズンの練習で、彼らは2度目のシーズンでMLS史上最高の攻撃チームの1つに爆変しました。
By varying the z-score to filter the data, you can look at the under-presented pass types and choose the degree of representation. In 2018, Columbus did not utilize long passes out of the back often, LAFC was less likely to cross from the flanks, and Portland didn’t pass from central locations back towards their own goal.
Z値を変化させてデータをフィルター処理することにより、不足しているパスタイプを確認し、表示の程度を選択できます。2018年、コロンバスは後方からの長いパスを頻繁に使用しませんでした。ロサンゼルスFCはサイドからあまりクロスを上げず、ポートランドは中央の位置から自分のゴールに向かってバックパスをしませんでした。
Tactical specialization
戦術的な特化
Using z-scores not only gives us a standardized score to evaluate the degree of representation of each pass cluster but also a quantitative measure of a team’s tactical specialization. Each z-score measures how much different a team is in using one type of passes compared to everyone else. If we take the median of the absolute value of the z-scores (since because both over- and under-representation equate to specialization, thanks for the idea, Dummy Run) per team, we approximate how much different a team is to everyone else.
Z値(標準得点)を使用すると、各パスクラスターの表現の程度を評価するための標準化されたスコアが得られるだけでなく、チームの戦術的特化の定量的尺度も得られます。各Z値は、あるタイプのパスを使用するチームが他のチームと比較してどれだけ異なるかを測定します。チームごとにZ値の絶対値の中央値をとると(過大表現と過小表現はどちらも特化と等価、Dummy Run氏のアイデア)、チームごとにチームがどれだけ違うかを近似します。
Specialization does not necessarily mean a team is good or bad. There is only a weak, but significant, correlation between specialization and expected goal difference (R = 0.24, p = 0.007). In fact, two of the most specialized teams (>99th percentile) in the last seven years are New York City FC in 2016 and Colorado in 2018. Their most over-represented pass types are those that couldn’t get across the half-line. They are basically specialized in not passing forward. A non-ideal method of winning games, to say the least. The full table of specialization scores is at the bottom of this post.
特化とは、必ずしもチームが良いか悪いかということではありません。特化とxG(Expected Goal)の差との間には、弱いが重要な相関関係があるだけです(R = 0.24、p = 0.007)。実際、過去7年間で最も特化されたチーム(99パーセンタイル以上)の2つは、2016年のニューヨークシティFCと2018年のコロラドです。最も過剰に表現されているパスタイプは、ハーフラインを越えることができなかったものです。彼らは基本的に、前パスをしないことに特化しています。控えめに言っても、ゲームに勝つには非理想的な方法です。特化スコアの完全な表は、この投稿の最後にあります。
The specialization scoring confirms some eye tests while refutes the others. For example, New York Red Bulls are believed to be the most distinctive franchise in MLS. The top five most distinctive teams from the last seven years include three Red Bulls, all under the supervision of Jesse Marsch (and Chris Armas last year). In contrast, many pundits believe that Columbus Crew under Gregg Berhalter played with a very unique style. However, their specialization scores suggest that they have been less specialized than most teams in the last four seasons. These are good examples of how an objective measure of style can help judge whether our subjective opinion stands.
特化スコアはいくつかの目視を確認する一方、他に反論します。例えば、ニューヨーク・レッドブルズはMLSで最も特徴的なフランチャイズと考えられています。過去7年間で最も特徴的な上位5チームには、3シーズンのレッドブルが含まれており、これらはすべてジェシー・マーズチ(および昨年のクリス・アルマス)の監督下にあります。これとは対照的に、多くの専門家はグレッグ・バーホルターの下のコロンバス・クルーが非常にユニークなスタイルでプレーしたと考えています。しかし彼らの特化スコアは、過去4シーズンでほとんどのチームよりも特化が劣っていることを示唆しています。これらは、スタイルの客観的な尺度が主観的な意見が正しいかどうかの判断にどのように役立つかを示す良い例です。
Coaching influences tactical systems
コーチングは戦術システムに影響を与える
The specialization score only tells us whether a team is different from everyone else, but it doesn’t tell us whether two teams are similar or not.Two teams can have very similar specialization scores but they can be specialized in different ways.Quantifying the way two teams play can tell us how coaching change or player turnover can impact the play style of the team.
特化スコアは、チームが他と異なるかどうかのみを示し、2つのチームが類似しているかどうかは示しません。2チームは非常に似た特化スコアを持ちますが、異なる方法でも特化することができます。2つのチームのプレー方法を定量化することで、コーチングの変化や選手の移籍がチームのプレースタイルにどのように影響するかを知ることができます。
To quantify the similarity of the play styles of the same team in two consecutive seasons, we calculate the Euclidean distance of the z-score for each cluster between seasons. We then do another z-score to standardize the resultant score and calculate a percentile to determine how the change between two years are compared to every other transition in the last seven seasons (note: above 50 is greater than average difference, below 50 less than average difference):
連続した2シーズンにおける同じチームのプレースタイルの類似性を定量化するため、シーズン間の各クラスタのzスコア(標準得点)のユークリッド距離を計算します。次に、得られたスコアを標準化するために別の標準得点を作成し、過去7シーズンの他の全推移と比較しての変化を決定するためのパーセンタイルを計算します(注:50以上は平均差より大きく、50以下は平均差より小さい)。
A coaching change seems to be the strongest driver in the evolution of the play style; even though the New York Red Bulls are the most distinctive franchise in the MLS, their style has been consistent under Marsch since 2016. Large differences in similarities were seen in Columbus when Gregg Berhalter took over for Robert Warzycha (2013-2014), NYCFC transitioning from Jason Kreis to Patrick Vieira (2015-2016), and New England in Brad Friedel’s first season (2017-2018) after years of below average change under Jay Heaps. However coaching changes don’t always bring change, Portland, San Jose, and LA Galaxy showed less than average change when moving to new coaches. Interestingly, since 2015, SKC has shown increased year-over-year differences under Peter Vermes. While Ben Olsen and Pablo Mastroeni showed wild swings year-to-year during their respective tenures at DC United and Colorado.
監督の変更は、プレースタイルの進化における最強の推進力と思われます。ニューヨーク・レッドブルズはMLSの中で最も独特のフランチャイズですが、そのスタイルは2016年以来ジェシー・マーズチの下で一貫しています。グレッグ・バーホルターがロベルト・ヴァジハ(2013-2014)から引き継いだ時のコロンブス、ジェイソン・クライスからパトリック・ヴィエラ(2015-2016)に移行したニューヨーク・シティFC、およびジェイ・ヒープスの下で平均以下の変化後のブラッド・フリーデルの最初のシーズン(2017-2018)のニューイングランドに、類似性に大きな違いが見られます。しかし、監督の変更が必ずしも変化をもたらすわけではなく、ポートランド、サンノゼ、およびLAギャラクシーは、新指揮官に移行したときに平均的な変化よりも少なかったです。興味深いことに2015年以来、SKCはピーター・バーミーズの下で年々の違いを示しています。ベン・オルセンとパブロ・マストロエニは、DCユナイテッドとコロラドでそれぞれの在任期間中に年々激しい変動を示しました。
Conclusion
結論
Our next steps will be to link our quantitative measurement of the style to some forms of performance index. For example, some teams may predominantly use a pass type, but at a low success rate.In that case, a coach may want to decide how important that cluster is for the team’s function. He or she may want to introduce a new training regimen to improve the performance of that pass type, use different players in those positions, or even alter the pass routes to bypass it. We can look at the outcome of the style by linking pass clustering with the pass chain concept and rate them with Expected Goal Chain. This way, we can find all groups of classes that produce the most damage for any team. Imagine three linked forward pass clusters in which the middle cluster is under-represented and sandwiched by two over-represented ones. Immediately you will know that the under-represented cluster is the weakest link; your team may use other actions such as dribbles or carries to move the ball through that area. The coach may want to instruct his/her players to pass more than they are doing. The opponent’s coach may want to hit that area or player.
次のステップは、スタイルの定量的測定を何らかの形のパフォーマンス指標に結び付けることです。たとえば、一部のチームは主にあるパスのタイプを使用しますが、成功率は低くなります。その場合、監督はそのクラスタがチームの機能にとってどれほど重要かを決定したいと思うかもしれません。そのパスの種類のパフォーマンスを向上させるために新しいトレーニングを導入したり、それらの位置で違った選手を使ったり、あるいはそれを回避するためにパスルートを変更したりしたいと思うかもしれません。パスクラスタとポゼッション連鎖の概念を結び付けてスタイルの結果を調べ、Expeted Goals Chainでそれらを評価できます。このようにして、どのチームにも最大のダメージを与えるクラスのすべてのグループを見つけることができます。3つのリンクされたフォワードパスクラスターを想像してください。このクラスターでは、中央のクラスターが過小表示され、2つの過大表示されたクラスターに挟まれています。すぐに、過小評価されたクラスターが最も弱いリンクであることがわかります。チームはドリブルしたり簡単にはたいたりしながら他のアクションを使用して、ボールをそのエリアに移動させることができます。監督は、自分のプレーヤーに、彼らが今やっている以上のパスをするように指示したいかもしれません。相手監督は、そのエリアや選手を襲いたいと思うかもしれない。
Applications like these are the tip of the iceberg in how this type of analysis can help coaching. Things like this can provide “actionable insights”, the holy grail of the soccer analytics.
このような応用は、このタイプの分析がコーチングにどのように役立つかについての氷山の一角です。
このようなことは、サッカー分析の聖杯である「実用的な洞察」を提供します。
以下は、2013年以降の各MLSシーズンのすべてのチームの過大評価されたパスクラスターと過小評価されたパスクラスター
| シーズン | チーム | 特化スコア | ランク |
|---|---|---|---|
| 2013 | Chicago | 1.47 | 10 |
| 2013 | Colorado | 0.08 | 48 |
| 2013 | Columbus | 1.41 | 12 |
| 2013 | DC United | -0.99 | 107 |
| 2013 | FC Dallas | -0.35 | 71 |
| 2013 | Houston | -0.99 | 108 |
| 2013 | Kansas City | -0.77 | 98 |
| 2013 | L.A. Galaxy | 0.43 | 34 |
| 2013 | Montreal | 1.54 | 9 |
| 2013 | New England | 0.57 | 29 |
| 2013 | New York | 0.27 | 40 |
| 2013 | Philadelphia | -0.06 | 53 |
| 2013 | Portland | -0.35 | 70 |
| 2013 | Salt Lake | -0.74 | 96 |
| 2013 | San Jose | 0.53 | 31 |
| 2013 | Seattle | -0.22 | 65 |
| 2013 | Toronto | -0.30 | 68 |
| 2013 | Vancouver | 0.22 | 44 |
| 2013 | Chivas | 1.04 | 17 |
| 2014 | Chicago | -0.70 | 92 |
| 2014 | Colorado | -0.77 | 99 |
| 2014 | Columbus | -0.11 | 59 |
| 2014 | DC United | -0.46 | 80 |
| 2014 | FC Dallas | -0.71 | 93 |
| 2014 | Houston | -0.46 | 79 |
| 2014 | Kansas City | -1.18 | 112 |
| 2014 | L.A. Galaxy | 1.78 | 7 |
| 2014 | Montreal | -0.40 | 76 |
| 2014 | New England | 1.67 | 8 |
| 2014 | New York | 0.26 | 41 |
| 2014 | Philadelphia | 1.13 | 16 |
| 2014 | Portland | -0.57 | 84 |
| 2014 | Salt Lake | -1.41 | 121 |
| 2014 | San Jose | 0.05 | 49 |
| 2014 | Seattle | 0.39 | 36 |
| 2014 | Toronto | -0.68 | 91 |
| 2014 | Vancouver | -0.93 | 104 |
| 2014 | Chivas | -0.72 | 94 |
| 2015 | Chicago | -1.28 | 116 |
| 2015 | Colorado | -1.14 | 109 |
| 2015 | Columbus | 2.17 | 6 |
| 2015 | DC United | 0.12 | 47 |
| 2015 | FC Dallas | -0.53 | 83 |
| 2015 | Houston | -0.10 | 57 |
| 2015 | Kansas City | -1.43 | 123 |
| 2015 | L.A. Galaxy | -1.20 | 113 |
| 2015 | Montreal | -0.61 | 87 |
| 2015 | New England | 1.19 | 15 |
| 2015 | New York | 0.39 | 35 |
| 2015 | New York City FC | -0.39 | 75 |
| 2015 | Orlando City | -0.33 | 69 |
| 2015 | Philadelphia | -0.07 | 54 |
| 2015 | Portland | 0.63 | 27 |
| 2015 | Salt Lake | -0.46 | 81 |
| 2015 | San Jose | -0.50 | 82 |
| 2015 | Seattle | 0.74 | 23 |
| 2015 | Toronto | 0.29 | 37 |
| 2015 | Vancouver | -0.08 | 55 |
| 2016 | Chicago | 0.65 | 26 |
| 2016 | Colorado | -1.17 | 111 |
| 2016 | Columbus | -0.20 | 64 |
| 2016 | DC United | 0.29 | 38 |
| 2016 | FC Dallas | -0.58 | 85 |
| 2016 | Houston | 0.22 | 45 |
| 2016 | Kansas City | -0.72 | 95 |
| 2016 | L.A. Galaxy | -1.35 | 120 |
| 2016 | Montreal | -1.15 | 110 |
| 2016 | New England | 1.36 | 13 |
| 2016 | New York | 2.48 | 4 |
| 2016 | New York City FC | 3.14 | 2 |
| 2016 | Orlando City | -0.61 | 86 |
| 2016 | Philadelphia | -0.16 | 60 |
| 2016 | Portland | -0.42 | 77 |
| 2016 | Salt Lake | 0.17 | 46 |
| 2016 | San Jose | -0.80 | 100 |
| 2016 | Seattle | -0.81 | 102 |
| 2016 | Toronto | -1.24 | 114 |
| 2016 | Vancouver | -0.09 | 56 |
| 2017 | Chicago | 0.46 | 33 |
| 2017 | Colorado | 0.77 | 22 |
| 2017 | Columbus | -0.61 | 88 |
| 2017 | DC United | -0.95 | 105 |
| 2017 | FC Dallas | -0.38 | 72 |
| 2017 | Houston | 0.69 | 24 |
| 2017 | Kansas City | -0.10 | 58 |
| 2017 | L.A. Galaxy | -1.33 | 119 |
| 2017 | Montreal | 0.57 | 30 |
| 2017 | New England | -0.85 | 103 |
| 2017 | New York | 2.31 | 5 |
| 2017 | New York City FC | 0.65 | 25 |
| 2017 | Orlando City | -0.38 | 73 |
| 2017 | Philadelphia | 0.29 | 39 |
| 2017 | Portland | -1.30 | 118 |
| 2017 | Salt Lake | -0.81 | 101 |
| 2017 | San Jose | -0.96 | 106 |
| 2017 | Seattle | -0.75 | 97 |
| 2017 | Toronto | -0.38 | 74 |
| 2017 | Vancouver | -0.06 | 52 |
| 2017 | Atlanta United | 0.24 | 43 |
| 2017 | Minnesota United | -0.17 | 62 |
| 2018 | Chicago | 0.82 | 21 |
| 2018 | Colorado | 2.91 | 3 |
| 2018 | Columbus | -0.19 | 63 |
| 2018 | DC United | -0.05 | 51 |
| 2018 | FC Dallas | -1.43 | 122 |
| 2018 | Houston | -0.65 | 90 |
| 2018 | Kansas City | 0.82 | 20 |
| 2018 | L.A. Galaxy | -1.28 | 117 |
| 2018 | Montreal | 0.52 | 32 |
| 2018 | New England | -0.25 | 66 |
| 2018 | New York | 3.79 | 1 |
| 2018 | New York City FC | 1.43 | 11 |
| 2018 | Orlando City | -0.04 | 50 |
| 2018 | Philadelphia | 0.96 | 18 |
| 2018 | Portland | -1.27 | 115 |
| 2018 | Salt Lake | 0.58 | 28 |
| 2018 | San Jose | -0.30 | 67 |
| 2018 | Seattle | 1.35 | 14 |
| 2018 | Toronto | 0.25 | 42 |
| 2018 | Vancouver | -0.44 | 78 |
| 2018 | Atlanta United | 0.86 | 19 |
| 2018 | Minnesota United | -0.62 | 89 |
Appendix
●MLS(Major League Soccer)
アメリカ合衆国とカナダのプロサッカーリーグ
●parking-the-bus
サッカーで使われるスラング。こういう感じの意味。お正月の番組で、俊輔や中澤が走るバスの窓にシュートをするというのは、それなりに背景があるってことですね(あのミッションは選手にとってかなりの難度があるということです)。
●t-SNE(t-distributed Stochastic Neighbor Embedding)
T-distributed Stochastic Neighbor Embedding (t-SNE) is a machine learning algorithm for visualization developed by Laurens van der Maaten and Geoffrey Hinton. It is a nonlinear dimensionality reduction technique well-suited for embedding high-dimensional data for visualization in a low-dimensional space of two or three dimensions. Specifically, it models each high-dimensional object by a two- or three-dimensional point in such a way that similar objects are modeled by nearby points and dissimilar objects are modeled by distant points with high probability.
t-SNEはLaurens van der Maaten氏とジェフリー・ヒントン氏によって開発された視覚化のための機械学習アルゴリズムです。これは、2次元または3次元の低次元空間に視覚化のため高次元データを埋め込むのに最適な非線形次元圧縮手法です。具体的には高い確率で、類似のオブジェクトが近くの点に、相違のオブジェクトが離れた点にモデル化されるように、各高次元オブジェクトを2次元または3次元の点でモデル化します。
The t-SNE algorithm comprises two main stages. First, t-SNE constructs a probability distribution over pairs of high-dimensional objects in such a way that similar objects have a high probability of being picked while dissimilar points have an extremely small probability of being picked. Second, t-SNE defines a similar probability distribution over the points in the low-dimensional map, and it minimizes the Kullback–Leibler divergence (KL divergence) between the two distributions with respect to the locations of the points in the map. Note that while the original algorithm uses the Euclidean distance between objects as the base of its similarity metric, this should be changed as appropriate.
t-SNEアルゴリズムは2つの主な段階を含みます。まずt-SNEは、類似のオブジェクトが拾われる可能性が高い一方で、相違の点が拾われる可能性が極めて小さいように、高次元のオブジェクトのペアにわたる確率分布を構築します。第二に、t-SNEは低次元マップ内の点にわたって同様の確率分布を定義し、それはマップ内の点の位置に関して2つの分布間のカルバック・ライブラー情報量を最小化します。元のアルゴリズムではオブジェクト間のユークリッド距離をその類似性指標のベースとして使用していますが、これは必要に応じて変更する必要があります。
t-SNE has been used for visualization in a wide range of applications, including computer security research, music analysis, cancer research, bioinformatics, and biomedical signal processing. It is often used to visualize high-level representations learned by an artificial neural network.
t-SNEはコンピュータセキュリティ研究、音楽分析、癌研究、生命情報科学、生物医学的信号処理など幅広い応用での視覚化に使用されてきました。人工ニューラルネットワークによって学習された高レベルの表現を視覚化するためによく使用されます。
While t-SNE plots often seem to display clusters, the visual clusters can be influenced strongly by the chosen parameterization and therefore a good understanding of the parameters for t-SNE is necessary. Such “clusters” can be shown to even appear in non-clustered data, and thus may be false findings. Interactive exploration may thus be necessary to choose parameters and validate results. It has been demonstrated that t-SNE is often able to recover well-separated clusters, and with special parameter choices, approximates a simple form of spectral clustering.
t-SNEプロットは多くの場合クラスタを表示するように見えますが、視覚的クラスタは選択されたパラメータ化によって強く影響される可能性があるため、t-SNEのパラメータをよく理解することが必要です。このような「クラスタ」は、非クラスタ化データにも現れることがあるため、誤った結果になる可能性があります。そのため、パラメータを選択して結果を検証するためには、対話型の探索が必要になる場合があります。t-SNEはよく分離されたクラスタを回復できることが多く、特別なパラメータを選択することで、単純な形のスペクトルクラスタリングに近いことが実証されています。
●elbow method(エルボー法)
エルボー法は、データセット内の適切なクラスタ数を見つけるのに役立つように設計されたクラスタ分析内での一貫性の解釈や検証の方法です。この方法では、クラスタ数の関数として説明された分散の割合を調べます。別のクラスタを追加してもデータのモデリングがそれほど良くならないように、いくつかのクラスタを選択する必要があります。
より正確には、クラスタ数に対してクラスタによって説明される分散の割合をプロットすると、最初のクラスタは多くの情報を追加しますが(多くの分散を説明する)、ある時点で差得が低下し、グラフの角度が変わります。この時点でクラスタ数が選択され、よって「エルボー基準」となります。この「エルボー」は常に明確に識別できるわけではありません。説明された分散の割合は、全分散に対する集団間の分散の比率で、F検定とも呼ばれます。この方法を少し変更すると、集団内分散の曲率がプロットされます。
●z値(z-score)
●パーセンタイル(percentile)
●カルバック・ライブラー情報量、ユークリッド距離
KL(Kullback–Leibler) Diverjence
●xG(Expected Goal)
フットボール・データアナリティクス:得点期待値に関する新指標「xG」についての解説








Leave a Reply