
数字を分類するニューラルネットワークの実装をやってみるではWindows + Python 2.xの環境でしたが、ここではubuntu 16.04 LTS + Python 3.xの環境です。
オリジナルコードはPython 2.x用でしたので、Python 3.x用に書き換えて実行してみます。
ディレクトリー構成はそのまま。
実行コードはmnist_loader.pyとnetwork.py。
2.x->3.xで変更する部分。
MNISTをロードするコード(mnist_loader.py)
import pickle as cPickle //変更
training_data, validation_data, test_data = cPickle.load(f,encoding=’latin1′) //encodeを追加
学習用のコード(network.py)
print関数
if test_data:
print (“Epoch {0}: {1} / {2}”.format(
j, self.evaluate(test_data), n_test)) //変更
else:
print (“Epoch {0} complete”.format(j)) //変更
len関数(zipに対してlenを適用….これでいけると思うんですが)
if test_data:
test_data = list(test_data) //追加
n_test = len(test_data)
training_data = list(training_data)//追加
n = len(training_data)
xrange
xrange -> range //変更
入力層784(28×28)・30世代(Epoch)・ミニバッチサイズ10・学習率η=3.0
で学習してみます。
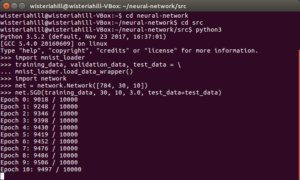
srcディレクトリに入って、Pyhon3のシェルを起動
$python3
>>>import mnist_loader
>>>training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
>>>import network
>>>net = network.Network([784, 30, 10])
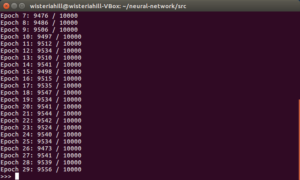
>>>net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
悪くないけど良くもない結果。
network.py
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
import random import numpy as np class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] def feedforward(self, a): for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): if test_data: test_data = list(test_data) n_test = len(test_data) training_data = list(training_data) n = len(training_data) for j in range(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in range(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print ("Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test)) else: print ("Epoch {0} complete".format(j)) def update_mini_batch(self, mini_batch, eta): nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] activation = x activations = [x] zs = [] for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) delta = self.cost_derivative(activations[-1], y) * \ sigmoid_prime(zs[-1]) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) for l in range(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def evaluate(self, test_data): test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data] return sum(int(x == y) for (x, y) in test_results) def cost_derivative(self, output_activations, y): return (output_activations-y) def sigmoid(z): return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): return sigmoid(z)*(1-sigmoid(z)) |
mnist_loader.py
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
import pickle as cPickle import gzip import numpy as np def load_data(): f = gzip.open('../data/mnist.pkl.gz', 'rb') training_data, validation_data, test_data = cPickle.load(f,encoding='latin1') f.close() return (training_data, validation_data, test_data) def load_data_wrapper(): tr_d, va_d, te_d = load_data() training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] training_results = [vectorized_result(y) for y in tr_d[1]] training_data = zip(training_inputs, training_results) validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]] validation_data = zip(validation_inputs, va_d[1]) test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]] test_data = zip(test_inputs, te_d[1]) return (training_data, validation_data, test_data) def vectorized_result(j): e = np.zeros((10, 1)) e[j] = 1.0 return e |
Leave a Reply