四元数：クォータニオン(Quaternion) メモ

 

---

三次元空間中での回転を簡単に記述できます。

ただ四元数の演算では交換則が成り立たないので、掛け算は結構面倒。

四元数はいろいろなところで使われていますが、このサイトでいうとGoogle VR Viewのホットスポット（embed.js）などで使用。quaternion計算用ライブラリーもthree.jsに実装されています。

例として、3D空間内の１点を、ある軸の周りで任意の角度で回転させてみます。

---

四元数の意味

実数は直線上の点を，複素数は平面上の点を表すものに対して、四元数は空間内の点を記述するもので、複素数を拡張したもの。

直線上の点には実数(a)を対応させる、平面上の点つまり座標(a,b)には複素数(a + bi)を対応させる、空間の点の座標には四元数を対応させる…という考え方

---

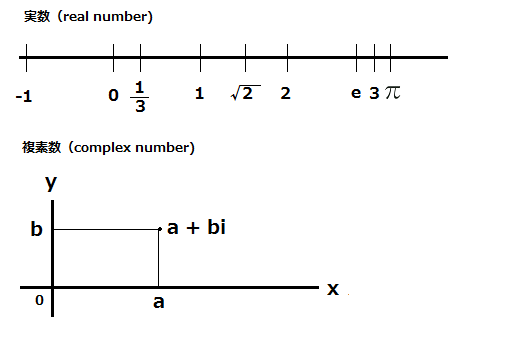
四元数（quaternion)

 

$$i^2 = -1 , j^2 = -1 , k^2 =-1 , ijk = -1\\ ij = k , jk = i , ki = j \hspace{ 73pt }\\ ji = -k , kj = -i , ik = -j\hspace{ 53pt }$$

 

四元数のノルム

$$\| q \| = \sqrt{a^2 + b^2 + c^2 + d^2}$$

共役な四元数

$$\overline{q}  = a – bi – cj – dk$$

逆数（逆元）

$$q^{-1}q = q q^{-1} = 1   となる元q^{-1}\\具体的には q^{-1} = \frac{\overline q}{\| q \|^2} \hspace{28pt}$$

 

 

四元数は積に関して交換則が成立しない、従って掛け算はどっちから掛けるかが重要になる（四元数単位の順序が逆だと符号も逆になる）

ij = k　,　ji = −k

四元数は結合則を満たす

$$q_1(q_2 q_3) = (q_1 q_2)q_3$$

四元数は分配則を満たす

$$q_1(q_2 + q_3) = q_1q_2 + q_1q_3 $$

積の共役は,共役の積（ただし順番は逆）

$$\overline{q_1q_2} = \overline {q_2} \hspace{2pt} \overline {q_1}$$

---

3次元座標空間における任意の点は、3次元位置ベクトルP = (x, y, z)で示されます。この3次元ベクトルは、以下のようにスカラー部を0とした四元数で表すことができます。

q=0+xi+yj+zk = xi + yj + zk

---

回転軸の方向ベクトル

$$\vec{u} =  (u_x,u_y,u_z)   \\  |\vec{u}| = 1\hspace{40pt}$$

ベクトルの方向に対して、時計回り・右ネジ周りにθの回転を考える

回転に対応する四元数は以下のとおり

$$q = cos \frac{θ}{2} + (u_x i + u_y j + u_z k) sin\frac{θ}{2} $$

この時

$$ベクトル \vec a = (a_x,a_y,a_z)が四元数 q = a_xi + a_yj + a_zkに対応するとすると、$$

$$\vec aをqが定める回転角によって回転させると、四元数\bf b = qa\overline q \hspace{63pt}$$

が成り立つ

---

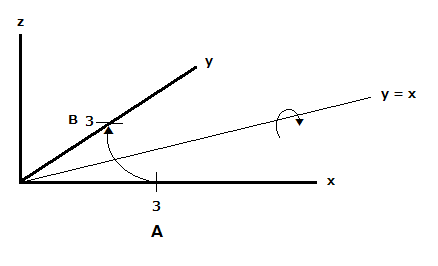
点A(3,0,0)をy = x,z = 0で表される直線の周りを180°回転させた点Bの座標を求めてみます。

 

 

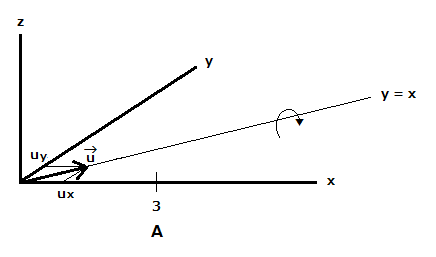
点Aに対応する四元数は、a =  0 + 3i + oj + 0k = 3i

$$u_x = v , u_y = v , u_z = 0 \hspace{90pt}\\ \vec u = (v,v,0) \hspace{130pt}\\ 方向ベクトルの大きさは１なので\hspace{50pt}\\ | \vec u| = \sqrt{v^2 + v^2+ 0^2} = 1 \hspace{73pt}\\ 従って、 v = \frac{1}{\sqrt 2}\hspace{110pt}$$

$$回転軸の方向ベクトル\vec u = \left( \frac{1}{\sqrt 2},\frac{1}{\sqrt 2},0\right) \\ 対応する四元数は q = \frac{1}{\sqrt 2} (i + j) \hspace{35pt}$$

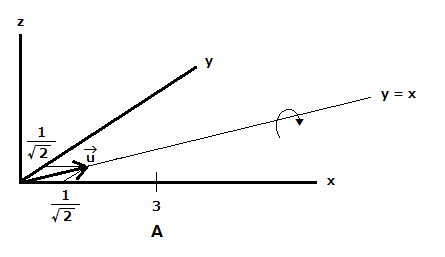
点Bに対応する四元数は以下のとおり

$$b = qa\overline q\hspace{100pt}$$

$$\begin{eqnarray} b &=& \frac{1}{\sqrt 2}(i + j)(3i)\frac{1}{\sqrt 2}(-i-j)\\&=& \frac{(i + j)(3i)(-i-j)}{2}\\&=& \frac{(3i^2 + 3ji)(-i-j)}{2}\\&=& \frac{-3i^3 – 3i^2j – 3ji^2 – 3jij}{2}\\&=& \frac{3i + 3j + 3j + 3ij^2}{2}\\&=& \frac{3i + 3j + 3j -3i}{2}\\&=& 3j \end{eqnarray}$$

 

Bの座標は(0,3,0)

---

Appendix1

クォータニオン計算便利ノート

 

---