
数字を分類するニューラルネットワークの実装をやってみる2-1の続きです。
GitHubにあるnetwork2.pyをやってみます。
network2.pyでは
MNISTの分類にクロス(交差)エントロピーを使っています。
ubuntu 16.04 LTS + Python 3.x用にnetwork2.pyを修正。
$python3
>>>import mnist_loader
>>>training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
>>>import network2
>>>net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>>net.large_weight_initializer()
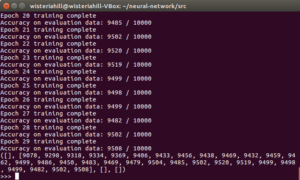
>>>net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data,
monitor_evaluation_accuracy=True)
network2.py
学習したモデルはsave()関数で保存できます。
>>>net.save(“nn2”)
ネットワークモデル、重み、バイアス、コスト関数名がJSON形式で保存されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 |
import json import random import sys import numpy as np class QuadraticCost(object): @staticmethod def fn(a, y): return 0.5*np.linalg.norm(a-y)**2 @staticmethod def delta(z, a, y): return (a-y) * sigmoid_prime(z) class CrossEntropyCost(object): @staticmethod def fn(a, y): return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): return (a-y) class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost def default_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def large_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def feedforward(self, a): for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, lmbda = 0.0, evaluation_data=None, monitor_evaluation_cost=False, monitor_evaluation_accuracy=False, monitor_training_cost=False, monitor_training_accuracy=False): if evaluation_data: evaluation_data = list(evaluation_data) n_data = len(evaluation_data) training_data = list(training_data) n = len(training_data) evaluation_cost, evaluation_accuracy = [], [] training_cost, training_accuracy = [], [] for j in range(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in range(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch( mini_batch, eta, lmbda, len(training_data)) print ("Epoch %s training complete" % j) if monitor_training_cost: cost = self.total_cost(training_data, lmbda) training_cost.append(cost) print ("Cost on training data: {}".format(cost)) if monitor_training_accuracy: accuracy = self.accuracy(training_data, convert=True) training_accuracy.append(accuracy) print ("Accuracy on training data: {} / {}".format( accuracy, n)) if monitor_evaluation_cost: cost = self.total_cost(evaluation_data, lmbda, convert=True) evaluation_cost.append(cost) print ("Cost on evaluation data: {}".format(cost)) if monitor_evaluation_accuracy: accuracy = self.accuracy(evaluation_data) evaluation_accuracy.append(accuracy) print ("Accuracy on evaluation data: {} / {}".format( self.accuracy(evaluation_data), n_data)) print return evaluation_cost, evaluation_accuracy, \ training_cost, training_accuracy def update_mini_batch(self, mini_batch, eta, lmbda, n): nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] activation = x activations = [x] zs = [] for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) delta = (self.cost).delta(zs[-1], activations[-1], y) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) for l in range(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def accuracy(self, data, convert=False): if convert: results = [(np.argmax(self.feedforward(x)), np.argmax(y)) for (x, y) in data] else: results = [(np.argmax(self.feedforward(x)), y) for (x, y) in data] return sum(int(x == y) for (x, y) in results) def total_cost(self, data, lmbda, convert=False): cost = 0.0 for x, y in data: a = self.feedforward(x) if convert: y = vectorized_result(y) cost += self.cost.fn(a, y)/len(data) cost += 0.5*(lmbda/len(data))*sum( np.linalg.norm(w)**2 for w in self.weights) return cost def save(self, filename): data = {"sizes": self.sizes, "weights": [w.tolist() for w in self.weights], "biases": [b.tolist() for b in self.biases], "cost": str(self.cost.__name__)} f = open(filename, "w") json.dump(data, f) f.close() def load(filename): f = open(filename, "r") data = json.load(f) f.close() cost = getattr(sys.modules[__name__], data["cost"]) net = Network(data["sizes"], cost=cost) net.weights = [np.array(w) for w in data["weights"]] net.biases = [np.array(b) for b in data["biases"]] return net def vectorized_result(j): e = np.zeros((10, 1)) e[j] = 1.0 return e def sigmoid(z): return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): return sigmoid(z)*(1-sigmoid(z)) |
Leave a Reply